Venn Diagram Independent Events Equation

Beginning with the multiplication rule for independent events.

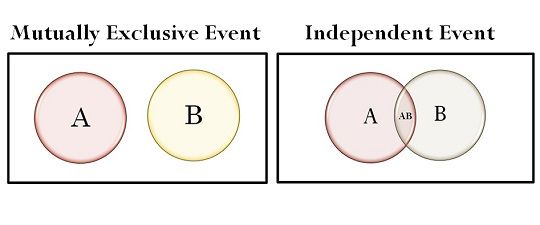
Venn diagram independent events equation. A venn diagram named after john venn in the 19th century provide a convenient way to represent a sample space. A set is a collection of things. Using a venn diagram we can visualize a and b which is represented by the overlap between events a and b. In a venn diagram the sets do not overlap each other in the case of mutually exclusive events while if we talk about independent events the sets overlap.

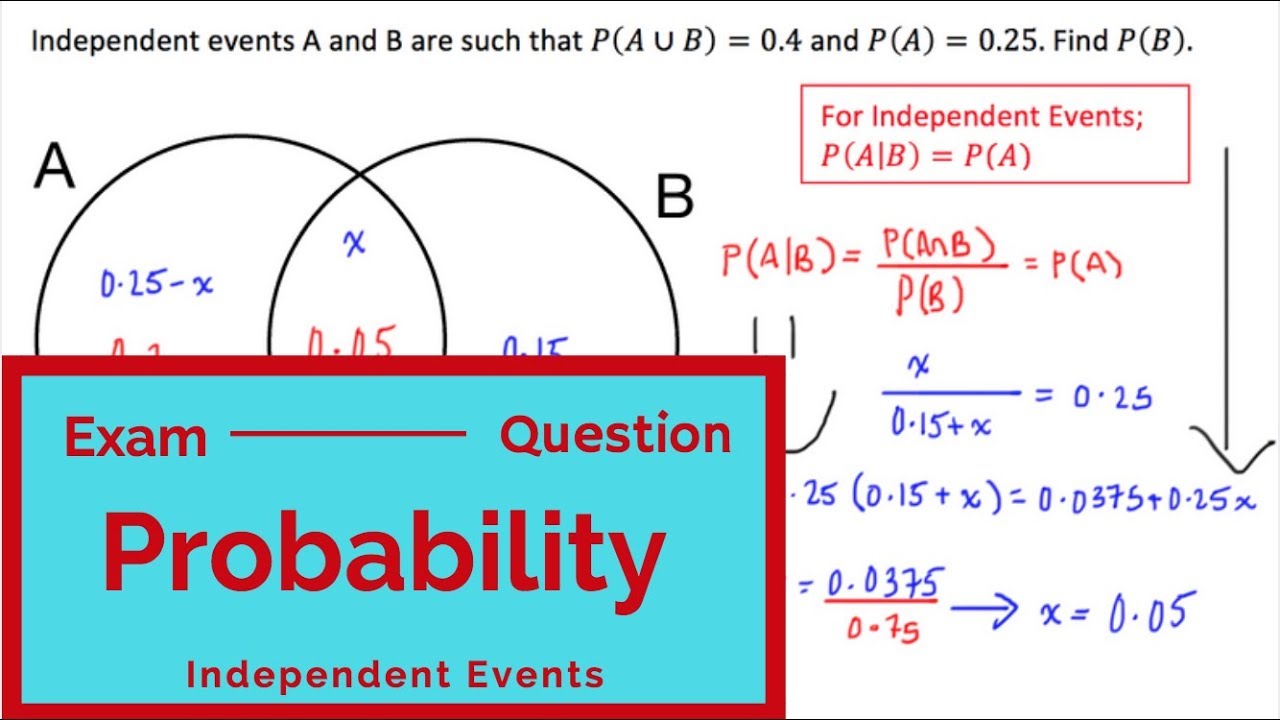
The overlapping set equation is tremendously important on the gmat. Two events e and f are independent. The best way to explain how the venn diagram works and what its formulas show is to give 2 or 3 circles venn diagram examples and problems with solutions. If x and y are independent events then the events x and y are also independent.

The idea of independent events is about whether or not the events affect each other in the sense that the occurrence of one event affects the probability of the. The key step is that pr e int f. Click here to remind yourself of what a sample space is. This is the lesser known but superior way to draw a venn diagram because it clearly defines the region of things that are members of neither set inside neither circle.

These include hat shirt jacket pants and so on. For example the items you wear is a set. Mutually exclusive events are represented mathematically as p a and b 0 while independent events are represented as p a and b p a p b. Let us draw a venn diagram for this condition.

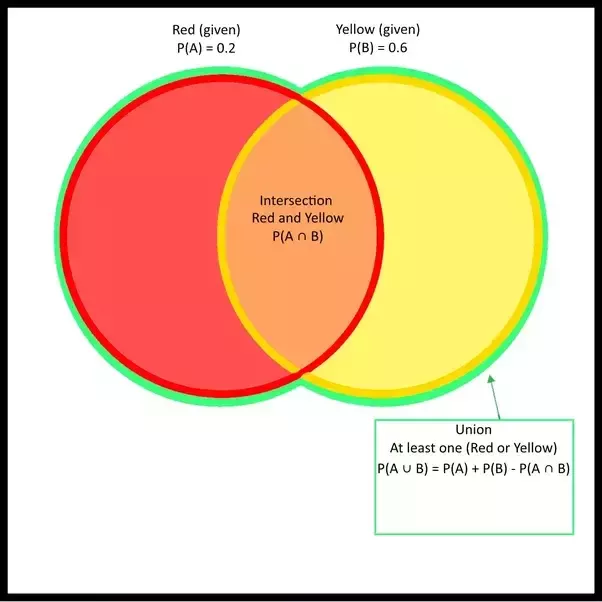
Pr e 6 and pr f 5. Sets and venn diagrams sets. Problem solving using venn diagram is a widely used approach in many areas such as statistics data science business set theory math logic and etc. Let us proof the condition of independent events using a venn diagram.

You write sets inside curly brackets like this. Fill in the two event venn diagram for e and f. A venn diagram is a rectangle representing the whole space and circles inside representing various subspaces.