Properties Of Intersection Of Sets With Examples

Basically we find a b by looking for all the elements a and b have in common.

Properties of intersection of sets with examples. It is denoted by a b and is read a union b. To make it easy notice that what they have in common is in bold. Let a 3 7 11 and b x. Scroll down the page for examples and solutions.

In theorem 5 30 we will prove some properties of set operations for indexed families of sets. The algebra of sets defines the properties and laws of sets the set theoretic operations of union intersection and complementation and the relations of set equality and set inclusion it also provides systematic procedures for evaluating expressions and performing calculations involving these operations and relations. Forming the symmetric difference of two sets is simple but forming the symmetric difference of three sets is a bit trickier. But certainly expertise to solve the problem special tools techniques and tricks as well as knowledge of all the basic concepts are required to obtain a solution following are some of the operations that are performed on the sets.

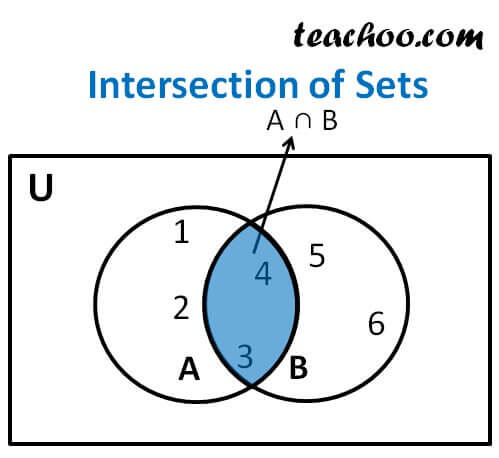
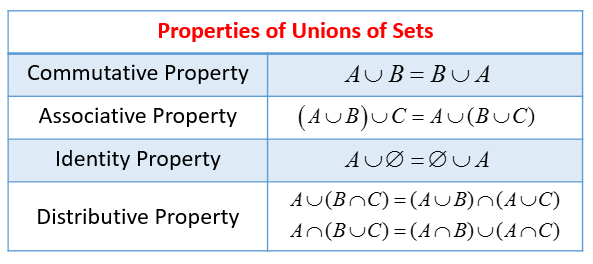
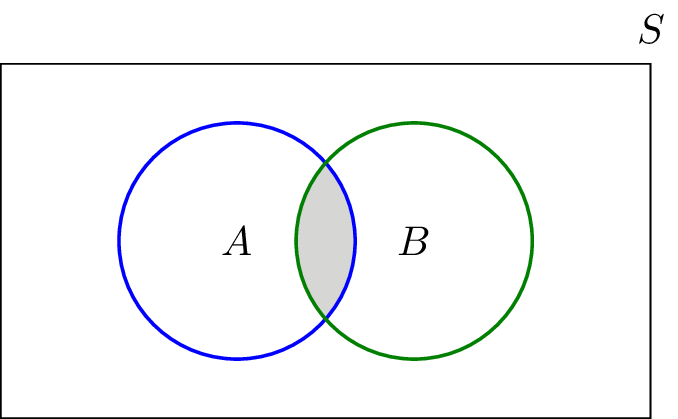
Intersection of sets a b has all the elements which are common to set a and set bit is represented by symbol let a 1 2 3 4 b 3 4 5 6 a b 3 4 the blue region is a bproperties of intersectiona b b a commutative law a b c a b c associative law a. Some of these properties are direct extensions of corresponding properties for two sets. Given two sets a and b the intersection is the set that contains elements or objects that belong to a and to b at the same time. We write a b.

The intersection property of the empty set says that any set intersected with the empty set gives the empty set. Properties of union and intersection. Unlike the real world operations mathematical operations do not require a separate no contamination room surgical gloves and masks. The union of two sets a and b is the set of elements which are in a or in b or in both.

The intersection of two sets a and b denoted by a b is the set of all elements that is common to both a and b. The following table gives some properties of union of sets. For example we have already proved de morgan s laws for two sets in theorem 5 20. For example a mathematician might be interested in knowing about sets s and t without caring at all whether the two sets are made of baseballs books letters or numbers.

In mathematical form for two sets a and b a b x. Any set of sets closed under the set theoretic operations forms a. Commutative associative identity and distributive. X is a natural number less than 0.

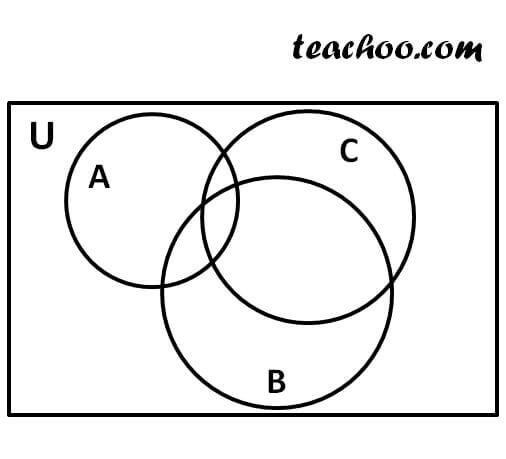
X a and x b similarly for three sets a b and c. A a. The following venn diagrams show the complement of the intersection of two sets and the complement of the intersection of three sets.