Not Disjoint Venn Diagram

Disjoint of sets using venn diagram is shown by two non overlapping closed regions and said inclusions are shown by showing one closed curve lying entirely within another.

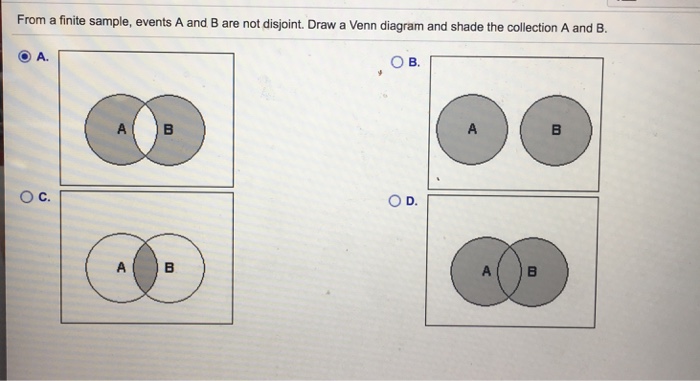
Not disjoint venn diagram. Events a and b are disjoint when they can t happen at the same time. Drawing a set outside of any other sets shows disjoint on a venn diagram. Some properties of operation of intersection. The venn diagram is now used in many fields including mathematics.

For example the numbers 2 4 and 6 are distinct objects when considered separately. Set theory sets theory representation of a set types of sets. A and b join together to make a b as shown in the venn diagram. Only your friends that play soccer or tennis or both.

Discussion of venn diagrams disjoint event and independent events. The venn diagram was introduced by john venn. P 1 3 5 7 11 13 and q january february march are disjoint because they have no element in common. A and b are disjoint when p a b 0.

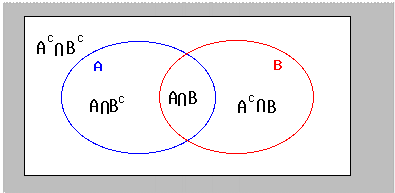
In each venn diagram is the universal set and a. The arrangement of the objects in the set does not matter. Let s take a look at john venn s idea. We can show that in a venn diagram.

The venn diagram was introduced by john venn. In other words we combine the elements of the two sets. Not everyone is in that set. His idea was to show sets in terms of pictures.

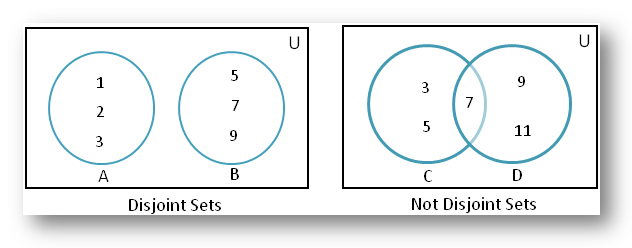
Subset disjoint overlap intersection union. For example let a 2 4 6 8 and b 1 3 5 7. In the venn diagram their areas are not connected. The disjoint sets can be represented by means of venn diagram as shown in the fig 1 6 in the above diagram a and b are disjoint sets.

Then a and b are disjoint sets because there are no elements which are common to a and b. In english language things are disjoint when they re not connected. Intersection of two disjoint sets is always the empty set. The following diagrams show the set operations and venn diagrams for complement of a set disjoint sets subsets intersection and union of sets.

Yes the venn diagram is named after a real person. In mathematics a set is a well defined collection of distinct objects considered as an object in its own right. The set of all elements being considered is called the universal set u and is represented by a rectangle. A set may be denoted by placing its objects between a pair of curly braces.

In each venn diagram is the universal set and a b and c are the sub sets of. P does not intersect k or p intersects k the empty set. When considered collectively they form a single set of size. Union of 2 sets.

Scroll down the page for more examples and solutions.