Diagram Venn A Gabungan B Komplemen

Definisi dari diagram venn adalah gambar himpunan yang menyatakan beberapa himpunan dan gabungan diantara beberapa himpunan.

Diagram venn a gabungan b komplemen. Perhatikan diagram venn di bawah ini daerah yang diarsir adalah komplemen dari a atau a. Himpunan merupakan kumpulan benda atau objek yang didefinisikan dengan jelas. Diagram venn diagram venn diperkenalkan oleh seorang ahli matematika asal inggris pada tahun 1834 1923. Dengan diagram venn a b bisa dinyatakan seperti pada gambar berikut ini.

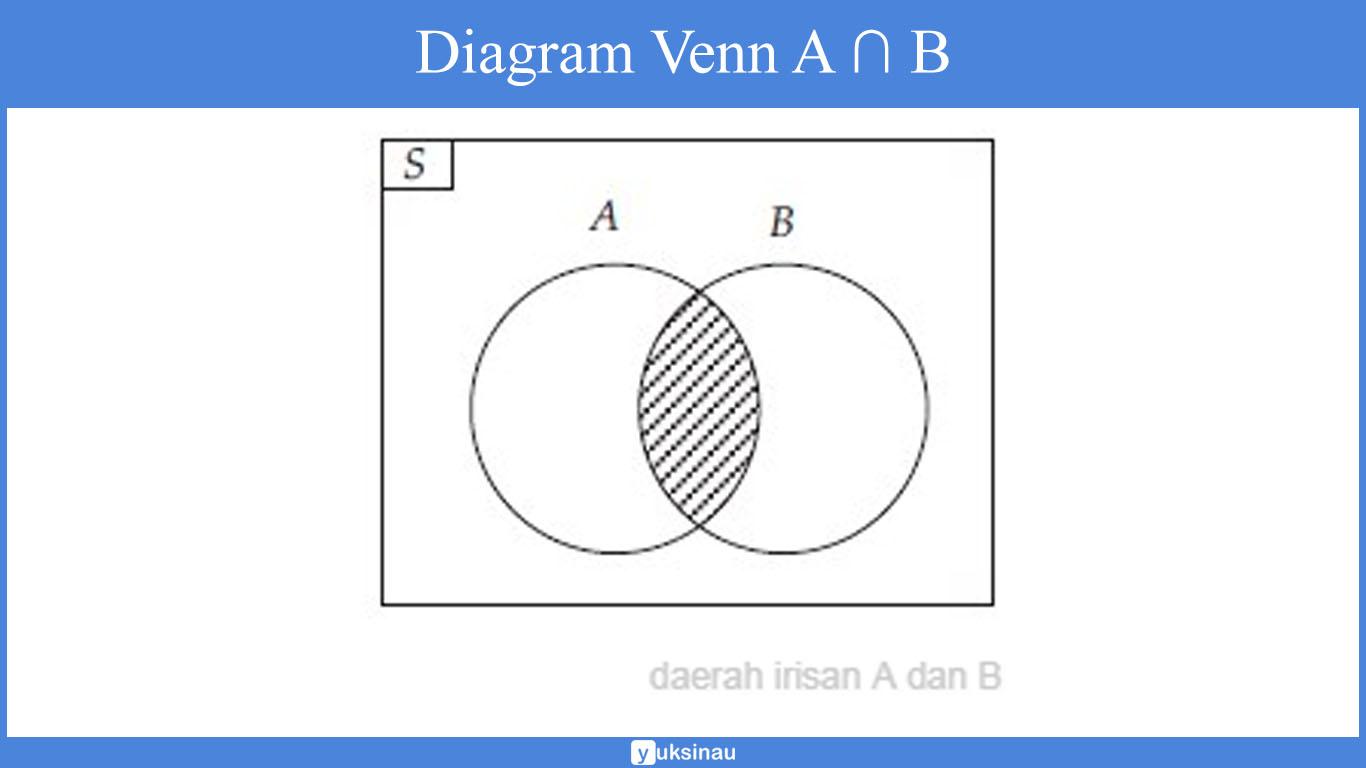
A b b c a b dibaca himpunan a irisan himpunan b. 15 a 1 3 5 7 9 11 13 b himpunan bilangan kelipatan tiga yang kurang dari 17 b 3 6 9 12 15. Dilihat dari persekutuan dua himpunan irisan dua himpunan dapat ditentukan. Dalam diagram venn ada empat hubungan antara himpunan termasuk gabungan irisan komplemen himpunan dan selisih dalam himpunan.

Komplemen himpunan a adalah suatu himpunan yang anggotaanggotanya merupakan anggota s tetapi bukan anggota a. Belajar komplemen himpunan dengan video dan kuis interaktif. Diagram venn merupakan cara untuk menyatakan himpunan dengan gambar diagram. Komplemen suatu himpunan agar anda dapat memahami mengenai komplemen suatu himpunan coba ingat kembali pengertian himpunan semesta atau semesta pembicaraan.

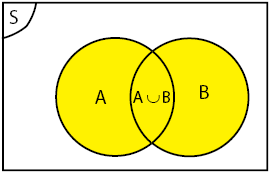
Himpunan a dan b adalah setara jika jumlah anggota dari dua himpunan tersebut adalah sama. Yang jika dinyatakan dalam diagram venn sebagai berikut. Dengan notasi pembentuk himpunan dituliskan sebagai berikut. Misalnya a dan b merupakan sebuah himpunan maka a b x x a atau x b.

Contoh soal operasi himpunan komplemen contoh soal perampatan operasi himpunan. Karena penemunya bernama jhon venn yang dimana venn tersebut diambil dari nama belakang penemu diagram tersebut. Komplemen dari a terhadap s ditulis a baca komplemen dari a atau a komplemen. N a n b.

Dapatkan pelajaran soal rumus komplemen himpunan lengkap di wardaya college. Gabungan adalah himpunan semua objek yang merupakan anggota a atau anggota b. Himpunan yang satu merupakan himpunan bagian yang lain jika maka dan berlaku sebaliknya himpunan yang sama jika a b maka himpunan yang saling lepas jika. Irisan irisan a dan b adalah himpunan yang anggotanya merupakan anggota a sekaligus anggota b.

Dengan pembentuk notasi himpunan dapat dituliskan a x x î s x ï a. Oleh karena itu dapat dikatakan bahwa irisan himpunan a dan b adalah b dan c atau ditulis dengan. Hal ini menunjukan bahwa a dan b saling lepas atau a b. Hubungan himpunan dan diagram venn dapat dilihat pada gambar di bawah.

Pada kedua himpunan tersebut ada dua anggota yang sama yaitu b dan c. Lambangnya è secara matematika a è b didefinisikan sebagai x x î a dan x î b. A himpunan bilangan ganjil. Secara matematis ditulis.